Maîtriser les graphes de contraintes : Un guide simple de résolution de problèmes
Les graphes de contraintes sont des outils visuels inestimables pour résoudre les problèmes de satisfaction de contraintes (CSP) dans de nombreuses disciplines. Ce guide pratique décompose le processus de construction des graphes de contraintes en étapes claires et gérables, adaptées à la fois aux nouveaux venus et aux professionnels chevronnés. Nous examinerons les principaux éléments constitutifs des CSP - variables, domaines et contraintes - avant d'illustrer leur représentation graphique. L'acquisition de compétences en matière de graphes de contraintes vous permettra de résoudre efficacement des problèmes complexes en établissant des relations entre les variables et leurs valeurs potentielles.
Points clés
Les graphes de contraintes offrent une clarté visuelle pour les problèmes de satisfaction de contraintes.
Les variables contiennent des ensembles de domaines définissant les valeurs possibles qu'elles peuvent prendre.
Les contraintes établissent des règles régissant l'affectation des valeurs des variables.
Les nœuds des graphes correspondent aux variables, tandis que les arêtes représentent les contraintes.
La construction de graphes de contraintes met en évidence les interrelations entre les variables.
Principes fondamentaux des problèmes de satisfaction de contraintes
Comprendre les problèmes de satisfaction de contraintes
Les problèmes de satisfaction de contraintes (CSP) impliquent la recherche d'affectations de valeurs aux variables qui satisfont à des conditions spécifiques. Ces modèles mathématiques apparaissent dans tous les domaines de l'intelligence artificielle, de la recherche opérationnelle et du développement de logiciels. La compréhension des principes fondamentaux des CSP s'avère essentielle lorsqu'il s'agit d'aborder des problèmes à multiples facettes exigeant le respect simultané de plusieurs conditions. Chaque CSP comprend trois éléments essentiels :
- Les variables : Entités nécessitant l'attribution de valeurs
- Domaines : Ensembles de valeurs possibles pour chaque variable
- Contraintes : Règles limitant les affectations de variables valides
L'objectif ultime du CSP consiste à identifier les affectations de valeurs qui satisfont à toutes les contraintes imposées.
Considérons les applications de planification où les variables représentent des tâches, les domaines indiquent les créneaux horaires disponibles et les contraintes spécifient les dépendances entre les tâches. Le fait de formuler ces scénarios sous forme de CSP permet d'appliquer des algorithmes spécialisés pour générer des plannings conformes aux contraintes.
Spécification des variables et des domaines
Les variables constituent les éléments fondamentaux de tout CSP, représentant des quantités inconnues à déterminer. La notation conventionnelle utilise des étiquettes alphabétiques (A, B, C, etc.). Chaque variable est associée à un domaine, c'est-à-dire à l'ensemble des valeurs qu'elle peut prendre. Les domaines peuvent contenir des valeurs numériques, des symboles ou d'autres types de données.
Par exemple, un domaine numérique peut comprendre {1, 2, 3, 4}, ce qui limite les variables à ces quatre valeurs entières.
Lors de la définition des variables et des domaines, veillez à ce que les domaines reflètent avec précision des plages de valeurs réalistes pour les variables correspondantes. Une définition précise du domaine simplifie la résolution des problèmes en réduisant l'espace de recherche des solutions. Pour les scénarios de gestion des effectifs, les variables représentant le nombre d'employés doivent posséder des domaines de nombres entiers non négatifs. Une spécification claire des variables et des domaines constitue la base de la formulation ultérieure des contraintes et de la génération de solutions.
Comprendre les contraintes
Les contraintes établissent des règles relationnelles régissant les interactions entre les variables en spécifiant les combinaisons de valeurs autorisées. Ces restrictions capturent les exigences essentielles du problème tout en garantissant la validité de la solution. Les contraintes se manifestent sous diverses formes, notamment des expressions mathématiques, des énoncés logiques ou des représentations symboliques.
Les variétés de contraintes les plus courantes sont les suivantes
- Contraintes d'égalité : Elles imposent des valeurs identiques entre les variables (par exemple, A = D).
- Contraintes d'inégalité : imposent des valeurs différentes entre les variables (par exemple, A ≠ B)
- Contraintes de plage : Limitent les valeurs des variables à l'intérieur de limites spécifiées (par exemple, C
Construction de graphes de contraintes
Construction de graphes de contraintes
Les graphes de contraintes fournissent des représentations visuelles du CSP par le biais de nœuds (variables) et d'arêtes (contraintes). La création de tels graphes améliore la compréhension du problème et le développement de la stratégie de solution. Suivez les étapes de construction suivantes :
Création de nœuds : Générer des nœuds de graphe pour chaque variable, en les étiquetant de manière appropriée.
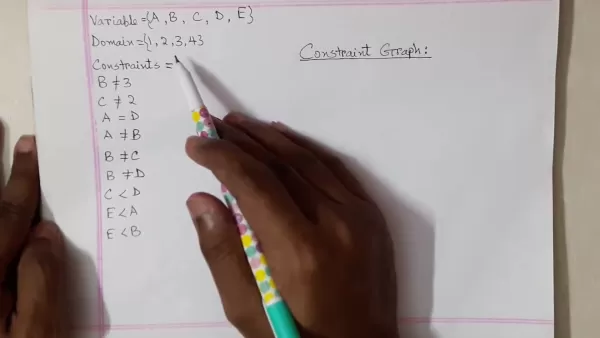
Mise en œuvre des arêtes : Relier les paires de variables contraintes par des arêtes étiquetées indiquant les types de contraintes.
Simplification du graphique : Optimiser le graphique en supprimant les arêtes redondantes et en consolidant les nœuds équivalents.
Ce processus permet d'obtenir une représentation visuelle du problème adaptée à l'application de divers algorithmes de résolution basés sur les graphes.
Analyse des graphes de contraintes
Les graphes de contraintes construits permettent une analyse perspicace du problème par le biais d'un examen structurel. L'analyse des graphes se concentre sur
- les composantes connectées : L'identification de sous-graphes indépendants permet de décomposer le problème.
- La détection des cycles : La reconnaissance des dépendances circulaires met en évidence la complexité du problème
- L'évaluation du degré : Les nœuds ayant de nombreuses arêtes représentent des variables critiques
Un examen approfondi du graphe révèle des informations précieuses sur le problème et permet d'élaborer des stratégies de solution efficaces par le biais d'une inspection visuelle et d'algorithmes spécialisés.
Guide de construction d'un graphe de contraintes
Étape 1 : Définition des variables et du domaine
Commencez par identifier explicitement toutes les variables du problème et établissez leurs domaines respectifs. Par exemple, les scénarios de coloriage de cartes désigneraient les régions comme des variables et les couleurs disponibles comme des domaines. Une spécification précise du domaine reflétant des options de valeur réalistes simplifie le développement ultérieur des contraintes.
Étape 2 : Formulation des contraintes
Élaborer des contraintes régissant les relations entre les variables au moyen d'expressions mathématiques ou logiques non ambiguës. Envisagez différents types de contraintes, notamment les contraintes d'égalité, d'inégalité et d'étendue, lorsque vous saisissez les exigences du problème.
Étape 3 : Représentation graphique
Traduire le CSP sous forme visuelle en construisant des nœuds pour les variables et des arêtes pour les contraintes. Employer des styles d'arêtes distincts pour les différents types de contraintes afin d'améliorer la lisibilité. Cette transformation des relations abstraites en une visualisation concrète facilite l'analyse du problème.
Étape 4 : Optimisation et analyse des graphes
Mettre en œuvre des techniques de simplification des graphes pour améliorer la clarté tout en conservant l'intégrité du problème. Appliquer l'analyse théorique des graphes pour identifier les possibilités de résolution des problèmes par le biais des composants connectés, des cycles et des nœuds critiques. Cet examen structuré permet de générer des solutions efficaces.
Considérations pratiques
Choix du logiciel CSP
Les outils de solution CSP vont des logiciels libres aux offres commerciales, avec des capacités variables. Les options libres conviennent aux applications expérimentales et à petite échelle, mais peuvent nécessiter une expertise technique. Les solutions commerciales offrent des fonctionnalités robustes à des prix correspondants, avec des modèles de tarification comprenant des licences basées sur l'utilisateur et des abonnements au nuage.
Avantages du graphe de contraintes
Les avantages sont les suivants
- Visualisation améliorée des problèmes
- Analyse simplifiée des relations
- Compatibilité avec les algorithmes de graphes
- Amélioration de la communication au sein de l'équipe
Limites du graphique des contraintes
Inconvénients potentiels :
- Temps de construction pour les problèmes de grande taille
- Exigences en matière d'expertise en théorie des graphes
- Difficultés liées à la représentation des contraintes complexes
- Encombrement visuel en cas d'interconnexions denses
Applications CSP
Implémentations dans le monde réel
Les CSP trouvent des applications dans de nombreux domaines :
- Ordonnancement : Optimisation du séquençage des tâches avec des contraintes
- Allocation des ressources : Distribution efficace de ressources limitées
- Configuration : Conception de systèmes répondant à des exigences spécifiques
- Planification : Développement de séquences d'action permettant d'atteindre des objectifs
Parmi les exemples concrets de mise en œuvre, on peut citer la planification des vols des compagnies aériennes, la gestion des ressources hospitalières, la planification des trajectoires robotiques et la configuration des systèmes informatiques.
Questions fréquemment posées
Quels sont les avantages des graphes de contraintes ?
Les graphes de contraintes offrent de multiples avantages, notamment une visualisation intuitive du problème, une analyse simplifiée des relations et une compatibilité avec les algorithmes de graphes établis. Le format visuel améliore la compréhension de la structure du problème et facilite l'identification d'approches de solutions efficaces.
Comment sélectionner les domaines variables ?
Pour sélectionner les domaines appropriés, il faut trouver un équilibre entre l'exhaustivité et la spécificité. Les domaines doivent englober toutes les valeurs valides possibles sans inclure d'options non valides, en tenant soigneusement compte de la nature des variables et des contraintes du problème.
Quelles sont les techniques qui permettent de résoudre efficacement les CSP ?
Les méthodes efficaces de résolution des CSP comprennent la recherche par retour en arrière, la propagation des contraintes et l'heuristique d'ordonnancement des variables. La combinaison de ces stratégies permet d'explorer efficacement l'espace des solutions tout en garantissant le respect des contraintes.
Article connexe
Révolutionner l'accès aux données : Le chat avec IA pour les bases de données relationnelles sans SQL
Une technologie d'IA révolutionnaire permet désormais à quiconque d'interagir avec des bases de données relationnelles en utilisant le langage de tous les jours - aucune connaissance spécialisée en SQ
Replit obtient un financement de 250 millions de dollars pour une valorisation de 3 milliards de dollars, renforçant ainsi sa domination dans le domaine du codage vibratoire.
Replit, la plateforme innovante qui a démocratisé le codage en intégrant le développement directement dans les navigateurs web, a obtenu un nouveau financement de 250 millions de dollars, catapultant
Le dernier modèle d'IA Gemini de Google affiche des scores de sécurité en baisse lors des tests
Les tests internes de Google révèlent des baisses de performance inquiétantes dans les protocoles de sécurité de son dernier modèle d'IA par rapport aux versions précédentes. Selon les nouveaux critèr
commentaires (0)
0/200
Les graphes de contraintes sont des outils visuels inestimables pour résoudre les problèmes de satisfaction de contraintes (CSP) dans de nombreuses disciplines. Ce guide pratique décompose le processus de construction des graphes de contraintes en étapes claires et gérables, adaptées à la fois aux nouveaux venus et aux professionnels chevronnés. Nous examinerons les principaux éléments constitutifs des CSP - variables, domaines et contraintes - avant d'illustrer leur représentation graphique. L'acquisition de compétences en matière de graphes de contraintes vous permettra de résoudre efficacement des problèmes complexes en établissant des relations entre les variables et leurs valeurs potentielles.
Points clés
Les graphes de contraintes offrent une clarté visuelle pour les problèmes de satisfaction de contraintes.
Les variables contiennent des ensembles de domaines définissant les valeurs possibles qu'elles peuvent prendre.
Les contraintes établissent des règles régissant l'affectation des valeurs des variables.
Les nœuds des graphes correspondent aux variables, tandis que les arêtes représentent les contraintes.
La construction de graphes de contraintes met en évidence les interrelations entre les variables.
Principes fondamentaux des problèmes de satisfaction de contraintes
Comprendre les problèmes de satisfaction de contraintes
Les problèmes de satisfaction de contraintes (CSP) impliquent la recherche d'affectations de valeurs aux variables qui satisfont à des conditions spécifiques. Ces modèles mathématiques apparaissent dans tous les domaines de l'intelligence artificielle, de la recherche opérationnelle et du développement de logiciels. La compréhension des principes fondamentaux des CSP s'avère essentielle lorsqu'il s'agit d'aborder des problèmes à multiples facettes exigeant le respect simultané de plusieurs conditions. Chaque CSP comprend trois éléments essentiels :
- Les variables : Entités nécessitant l'attribution de valeurs
- Domaines : Ensembles de valeurs possibles pour chaque variable
- Contraintes : Règles limitant les affectations de variables valides
L'objectif ultime du CSP consiste à identifier les affectations de valeurs qui satisfont à toutes les contraintes imposées.
Considérons les applications de planification où les variables représentent des tâches, les domaines indiquent les créneaux horaires disponibles et les contraintes spécifient les dépendances entre les tâches. Le fait de formuler ces scénarios sous forme de CSP permet d'appliquer des algorithmes spécialisés pour générer des plannings conformes aux contraintes.
Spécification des variables et des domaines
Les variables constituent les éléments fondamentaux de tout CSP, représentant des quantités inconnues à déterminer. La notation conventionnelle utilise des étiquettes alphabétiques (A, B, C, etc.). Chaque variable est associée à un domaine, c'est-à-dire à l'ensemble des valeurs qu'elle peut prendre. Les domaines peuvent contenir des valeurs numériques, des symboles ou d'autres types de données.
Par exemple, un domaine numérique peut comprendre {1, 2, 3, 4}, ce qui limite les variables à ces quatre valeurs entières.
Lors de la définition des variables et des domaines, veillez à ce que les domaines reflètent avec précision des plages de valeurs réalistes pour les variables correspondantes. Une définition précise du domaine simplifie la résolution des problèmes en réduisant l'espace de recherche des solutions. Pour les scénarios de gestion des effectifs, les variables représentant le nombre d'employés doivent posséder des domaines de nombres entiers non négatifs. Une spécification claire des variables et des domaines constitue la base de la formulation ultérieure des contraintes et de la génération de solutions.
Comprendre les contraintes
Les contraintes établissent des règles relationnelles régissant les interactions entre les variables en spécifiant les combinaisons de valeurs autorisées. Ces restrictions capturent les exigences essentielles du problème tout en garantissant la validité de la solution. Les contraintes se manifestent sous diverses formes, notamment des expressions mathématiques, des énoncés logiques ou des représentations symboliques.
Les variétés de contraintes les plus courantes sont les suivantes
- Contraintes d'égalité : Elles imposent des valeurs identiques entre les variables (par exemple, A = D).
- Contraintes d'inégalité : imposent des valeurs différentes entre les variables (par exemple, A ≠ B)
- Contraintes de plage : Limitent les valeurs des variables à l'intérieur de limites spécifiées (par exemple, C
Construction de graphes de contraintes
Construction de graphes de contraintes
Les graphes de contraintes fournissent des représentations visuelles du CSP par le biais de nœuds (variables) et d'arêtes (contraintes). La création de tels graphes améliore la compréhension du problème et le développement de la stratégie de solution. Suivez les étapes de construction suivantes :
Création de nœuds : Générer des nœuds de graphe pour chaque variable, en les étiquetant de manière appropriée.
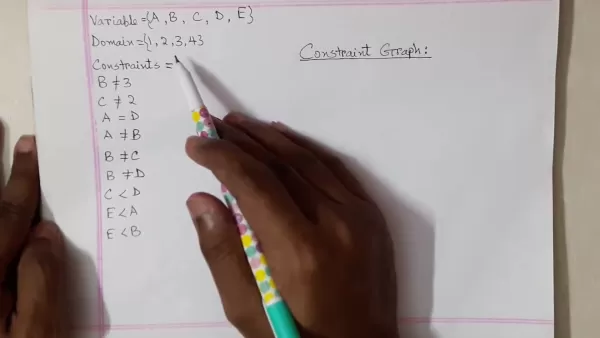
Mise en œuvre des arêtes : Relier les paires de variables contraintes par des arêtes étiquetées indiquant les types de contraintes.
Simplification du graphique : Optimiser le graphique en supprimant les arêtes redondantes et en consolidant les nœuds équivalents.
Ce processus permet d'obtenir une représentation visuelle du problème adaptée à l'application de divers algorithmes de résolution basés sur les graphes.
Analyse des graphes de contraintes
Les graphes de contraintes construits permettent une analyse perspicace du problème par le biais d'un examen structurel. L'analyse des graphes se concentre sur
- les composantes connectées : L'identification de sous-graphes indépendants permet de décomposer le problème.
- La détection des cycles : La reconnaissance des dépendances circulaires met en évidence la complexité du problème
- L'évaluation du degré : Les nœuds ayant de nombreuses arêtes représentent des variables critiques
Un examen approfondi du graphe révèle des informations précieuses sur le problème et permet d'élaborer des stratégies de solution efficaces par le biais d'une inspection visuelle et d'algorithmes spécialisés.
Guide de construction d'un graphe de contraintes
Étape 1 : Définition des variables et du domaine
Commencez par identifier explicitement toutes les variables du problème et établissez leurs domaines respectifs. Par exemple, les scénarios de coloriage de cartes désigneraient les régions comme des variables et les couleurs disponibles comme des domaines. Une spécification précise du domaine reflétant des options de valeur réalistes simplifie le développement ultérieur des contraintes.
Étape 2 : Formulation des contraintes
Élaborer des contraintes régissant les relations entre les variables au moyen d'expressions mathématiques ou logiques non ambiguës. Envisagez différents types de contraintes, notamment les contraintes d'égalité, d'inégalité et d'étendue, lorsque vous saisissez les exigences du problème.
Étape 3 : Représentation graphique
Traduire le CSP sous forme visuelle en construisant des nœuds pour les variables et des arêtes pour les contraintes. Employer des styles d'arêtes distincts pour les différents types de contraintes afin d'améliorer la lisibilité. Cette transformation des relations abstraites en une visualisation concrète facilite l'analyse du problème.
Étape 4 : Optimisation et analyse des graphes
Mettre en œuvre des techniques de simplification des graphes pour améliorer la clarté tout en conservant l'intégrité du problème. Appliquer l'analyse théorique des graphes pour identifier les possibilités de résolution des problèmes par le biais des composants connectés, des cycles et des nœuds critiques. Cet examen structuré permet de générer des solutions efficaces.
Considérations pratiques
Choix du logiciel CSP
Les outils de solution CSP vont des logiciels libres aux offres commerciales, avec des capacités variables. Les options libres conviennent aux applications expérimentales et à petite échelle, mais peuvent nécessiter une expertise technique. Les solutions commerciales offrent des fonctionnalités robustes à des prix correspondants, avec des modèles de tarification comprenant des licences basées sur l'utilisateur et des abonnements au nuage.
Avantages du graphe de contraintes
Les avantages sont les suivants
- Visualisation améliorée des problèmes
- Analyse simplifiée des relations
- Compatibilité avec les algorithmes de graphes
- Amélioration de la communication au sein de l'équipe
Limites du graphique des contraintes
Inconvénients potentiels :
- Temps de construction pour les problèmes de grande taille
- Exigences en matière d'expertise en théorie des graphes
- Difficultés liées à la représentation des contraintes complexes
- Encombrement visuel en cas d'interconnexions denses
Applications CSP
Implémentations dans le monde réel
Les CSP trouvent des applications dans de nombreux domaines :
- Ordonnancement : Optimisation du séquençage des tâches avec des contraintes
- Allocation des ressources : Distribution efficace de ressources limitées
- Configuration : Conception de systèmes répondant à des exigences spécifiques
- Planification : Développement de séquences d'action permettant d'atteindre des objectifs
Parmi les exemples concrets de mise en œuvre, on peut citer la planification des vols des compagnies aériennes, la gestion des ressources hospitalières, la planification des trajectoires robotiques et la configuration des systèmes informatiques.
Questions fréquemment posées
Quels sont les avantages des graphes de contraintes ?
Les graphes de contraintes offrent de multiples avantages, notamment une visualisation intuitive du problème, une analyse simplifiée des relations et une compatibilité avec les algorithmes de graphes établis. Le format visuel améliore la compréhension de la structure du problème et facilite l'identification d'approches de solutions efficaces.
Comment sélectionner les domaines variables ?
Pour sélectionner les domaines appropriés, il faut trouver un équilibre entre l'exhaustivité et la spécificité. Les domaines doivent englober toutes les valeurs valides possibles sans inclure d'options non valides, en tenant soigneusement compte de la nature des variables et des contraintes du problème.
Quelles sont les techniques qui permettent de résoudre efficacement les CSP ?
Les méthodes efficaces de résolution des CSP comprennent la recherche par retour en arrière, la propagation des contraintes et l'heuristique d'ordonnancement des variables. La combinaison de ces stratégies permet d'explorer efficacement l'espace des solutions tout en garantissant le respect des contraintes.
Révolutionner l'accès aux données : Le chat avec IA pour les bases de données relationnelles sans SQL
Une technologie d'IA révolutionnaire permet désormais à quiconque d'interagir avec des bases de données relationnelles en utilisant le langage de tous les jours - aucune connaissance spécialisée en SQ
Replit obtient un financement de 250 millions de dollars pour une valorisation de 3 milliards de dollars, renforçant ainsi sa domination dans le domaine du codage vibratoire.
Replit, la plateforme innovante qui a démocratisé le codage en intégrant le développement directement dans les navigateurs web, a obtenu un nouveau financement de 250 millions de dollars, catapultant
Le dernier modèle d'IA Gemini de Google affiche des scores de sécurité en baisse lors des tests
Les tests internes de Google révèlent des baisses de performance inquiétantes dans les protocoles de sécurité de son dernier modèle d'IA par rapport aux versions précédentes. Selon les nouveaux critèr
