Master Constraint Graphs: Um guia simples para a solução de problemas
Os gráficos de restrições são ferramentas visuais valiosas para resolver problemas de satisfação de restrições (CSPs) em várias disciplinas. Este guia prático divide o processo de construção de gráficos de restrições em etapas claras e gerenciáveis, adequadas tanto para iniciantes quanto para profissionais experientes. Examinaremos os principais blocos de construção dos CSPs - variáveis, domínios e restrições - antes de ilustrar sua representação gráfica. O desenvolvimento da proficiência em gráficos de restrições permite que você resolva problemas complexos com eficiência, mapeando as relações entre as variáveis e seus valores potenciais.
Pontos principais
Os gráficos de restrições oferecem clareza visual para desafios de satisfação de restrições
As variáveis contêm conjuntos de domínios que definem os possíveis valores que podem assumir
As restrições estabelecem regras que regem as atribuições de valores às variáveis
Os nós do gráfico correspondem a variáveis, enquanto as bordas denotam restrições
A construção de gráficos de restrições esclarece as inter-relações entre as variáveis
Fundamentos dos problemas de satisfação de restrições
Entendendo os problemas de satisfação de restrições
Os CSPs (Constraint Satisfaction Problems, problemas de satisfação de restrições) envolvem encontrar atribuições de valores a variáveis que satisfaçam condições específicas. Esses modelos matemáticos aparecem em toda a inteligência artificial, pesquisa operacional e desenvolvimento de software. A compreensão dos fundamentos dos CSPs é essencial quando se trata de problemas multifacetados que exigem o cumprimento simultâneo de várias condições. Todo CSP é composto por três elementos essenciais:
- Variáveis: Entidades que exigem atribuições de valores
- Domínios: Conjuntos de valores possíveis para cada variável
- Restrições: Regras que limitam as atribuições válidas de variáveis
O objetivo final do CSP envolve a identificação de atribuições de valores que satisfaçam todas as restrições impostas.
Considere os aplicativos de agendamento em que as variáveis representam tarefas, os domínios indicam os intervalos de tempo disponíveis e as restrições especificam as dependências das tarefas. Enquadrar esses cenários como CSPs permite a aplicação de algoritmos especializados para gerar programações compatíveis com as restrições.
Especificação de variáveis e domínios
As variáveis formam os elementos fundamentais em qualquer CSP, representando quantidades desconhecidas que exigem determinação. A notação convencional emprega rótulos em ordem alfabética (A, B, C etc.). Cada variável está associada a um domínio - o conjunto completo de valores permitidos que ela pode assumir. Os domínios podem conter valores numéricos, símbolos ou outros tipos de dados.
Por exemplo, um domínio numérico pode incluir {1, 2, 3, 4}, restringindo as variáveis a esses quatro valores inteiros.
Ao definir variáveis e domínios, certifique-se de que os domínios reflitam com precisão os intervalos de valores realistas das variáveis correspondentes. A definição precisa do domínio agiliza a solução de problemas ao restringir o espaço de busca de soluções. Nos cenários de gerenciamento da força de trabalho, as variáveis que representam a contagem de funcionários devem ter domínios inteiros não negativos. A especificação clara de variáveis e domínios estabelece a base para a formulação de restrições e a geração de soluções subsequentes.
Compreensão das restrições
As restrições estabelecem regras relacionais que regem as interações das variáveis, especificando combinações de valores permitidos. Essas restrições capturam os requisitos essenciais do problema e garantem a validade da solução. As restrições se manifestam de várias formas, incluindo expressões matemáticas, declarações lógicas ou representações simbólicas.
As variedades comuns de restrições incluem:
- Restrições de igualdade: Impõem valores idênticos entre variáveis (por exemplo, A = D)
- Restrições de desigualdade: Impõem valores diferentes entre as variáveis (por exemplo, A ≠ B)
- Restrições de intervalo: Limitam os valores das variáveis dentro dos limites especificados (por exemplo, C
Construção de gráficos de restrições
Construção de gráficos de restrições
Os gráficos de restrições fornecem representações visuais de CSP por meio de nós (variáveis) e bordas (restrições). A criação desses gráficos melhora a compreensão do problema e o desenvolvimento da estratégia de solução. Siga estas etapas de construção:
Criação de nós: Gere nós de gráficos para cada variável, rotulando-os adequadamente
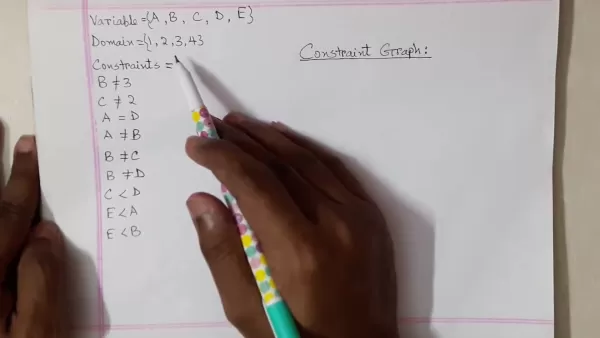
Implementação de bordas: Conecte os pares de variáveis restritas com bordas rotuladas indicando os tipos de restrição
Simplificação do gráfico: Otimizar o gráfico removendo bordas redundantes e consolidando nós equivalentes
Esse processo produz uma representação visual do problema adequada para a aplicação de vários algoritmos de solução baseados em gráficos.
Análise de gráficos de restrições
Os gráficos de restrições construídos permitem uma análise criteriosa do problema por meio de um exame estrutural. A análise do gráfico se concentra em:
- Componentes conectados: A identificação de subgrafos independentes permite a decomposição do problema
- Detecção de ciclos: O reconhecimento de dependências circulares destaca a complexidade do problema
- Avaliação do grau: Os nós com várias bordas representam variáveis críticas
O exame minucioso do gráfico revela insights valiosos sobre o problema, informando estratégias de solução eficazes por meio de inspeção visual e algoritmos especializados.
Guia de construção de gráficos de restrições
Etapa 1: Definição de variável e domínio
Comece identificando explicitamente todas as variáveis do problema e estabelecendo seus respectivos domínios. Por exemplo, cenários de coloração de mapas designariam regiões como variáveis e cores disponíveis como domínios. A especificação precisa do domínio, refletindo opções de valores realistas, simplifica o desenvolvimento subsequente de restrições.
Etapa 2: Formulação de restrições
Desenvolva restrições que regem as relações entre as variáveis por meio de expressões matemáticas ou lógicas não ambíguas. Considere vários tipos de restrições, incluindo igualdade, desigualdade e restrições de intervalo ao capturar os requisitos do problema.
Etapa 3: Renderização de gráficos
Traduza o CSP em formato visual construindo nós para variáveis e bordas para restrições. Empregue estilos de borda distintos para diferentes tipos de restrições para melhorar a legibilidade. Essa transformação de relações abstratas em visualização concreta facilita a análise do problema.
Etapa 4: otimização e análise de gráficos
Implemente técnicas de simplificação de gráficos para aumentar a clareza e, ao mesmo tempo, manter a integridade do problema. Aplique a análise teórica do gráfico para identificar oportunidades de solução de problemas por meio de componentes conectados, ciclos e nós críticos. Esse exame estruturado dá suporte à geração de soluções eficientes.
Considerações práticas
Seleção de software de CSP
As ferramentas de solução de CSP variam de ofertas de código aberto a ofertas comerciais com recursos variados. As opções de código aberto são adequadas para aplicações experimentais e de pequena escala, mas podem exigir conhecimento técnico especializado. As soluções comerciais oferecem funcionalidade robusta a preços correspondentes, com modelos de preços que incluem licenciamento baseado no usuário e assinaturas de nuvem.
Vantagens do Constraint Graph
Os benefícios incluem:
- Visualização aprimorada do problema
- Análise simplificada de relações
- Compatibilidade com algoritmos de gráficos
- Melhoria na comunicação da equipe
Limitações do Constraint Graph
Possíveis desvantagens:
- Tempo de construção para problemas grandes
- Requisitos de conhecimento em teoria dos grafos
- Desafios de representação de restrições complexas
- Desordem visual com interconexões densas
Aplicativos CSP
Implementações no mundo real
Os CSPs encontram aplicação em vários domínios:
- Agendamento: Otimização do sequenciamento de tarefas com restrições
- Alocação de recursos: Distribuição eficiente de ativos limitados
- Configuração: Projetar sistemas que atendam a requisitos específicos
- Planejamento: Desenvolvimento de sequências de ações para atingir objetivos
As implementações concretas incluem programação de linhas aéreas, gerenciamento de recursos hospitalares, planejamento de caminhos robóticos e configuração de sistemas de computador.
Perguntas frequentes
Quais são os benefícios dos gráficos de restrições?
Os gráficos de restrições oferecem várias vantagens, incluindo visualização intuitiva do problema, análise simplificada de relações e compatibilidade com algoritmos de gráficos estabelecidos. O formato visual aprimora a compreensão da estrutura do problema e facilita a identificação de abordagens de solução eficazes.
Como os domínios variáveis devem ser selecionados?
A seleção de domínios apropriados exige o equilíbrio entre abrangência e especificidade. Os domínios devem abranger todos os valores válidos possíveis sem incluir opções inválidas, considerando cuidadosamente a natureza da variável e as restrições do problema.
Quais técnicas resolvem CSPs de forma eficaz?
Os métodos eficazes de solução de CSPs incluem pesquisa de backtracking, propagação de restrições e heurística de ordenação de variáveis. A combinação dessas estratégias permite a exploração eficiente do espaço de solução e, ao mesmo tempo, garante a conformidade com as restrições.
Artigo relacionado
A IA revoluciona a genômica: AlphaGenome revela os segredos ocultos do DNA
Embora o DNA humano contenha aproximadamente 3 bilhões de letras genéticas, os cientistas decodificaram apenas uma fração desse projeto biológico. A maior parte do nosso genoma - particularmente os 98
8BitDo revela o controlador Pro 3 com botões intercambiáveis e personalizáveis
A 8BitDo revela seu aguardado controle sem fio Pro 3, marcando a primeira grande atualização desde o modelo Pro 2 de 2021. Diferentemente dos recentes layouts no estilo Nintendo vistos no controle Ult
Revolucionando o acesso aos dados: Chat alimentado por IA para bancos de dados relacionais sem SQL
A tecnologia revolucionária de IA agora permite que qualquer pessoa interaja com bancos de dados relacionais usando linguagem cotidiana, sem necessidade de conhecimento especializado em SQL. Essa abor
Comentários (0)
0/200
Os gráficos de restrições são ferramentas visuais valiosas para resolver problemas de satisfação de restrições (CSPs) em várias disciplinas. Este guia prático divide o processo de construção de gráficos de restrições em etapas claras e gerenciáveis, adequadas tanto para iniciantes quanto para profissionais experientes. Examinaremos os principais blocos de construção dos CSPs - variáveis, domínios e restrições - antes de ilustrar sua representação gráfica. O desenvolvimento da proficiência em gráficos de restrições permite que você resolva problemas complexos com eficiência, mapeando as relações entre as variáveis e seus valores potenciais.
Pontos principais
Os gráficos de restrições oferecem clareza visual para desafios de satisfação de restrições
As variáveis contêm conjuntos de domínios que definem os possíveis valores que podem assumir
As restrições estabelecem regras que regem as atribuições de valores às variáveis
Os nós do gráfico correspondem a variáveis, enquanto as bordas denotam restrições
A construção de gráficos de restrições esclarece as inter-relações entre as variáveis
Fundamentos dos problemas de satisfação de restrições
Entendendo os problemas de satisfação de restrições
Os CSPs (Constraint Satisfaction Problems, problemas de satisfação de restrições) envolvem encontrar atribuições de valores a variáveis que satisfaçam condições específicas. Esses modelos matemáticos aparecem em toda a inteligência artificial, pesquisa operacional e desenvolvimento de software. A compreensão dos fundamentos dos CSPs é essencial quando se trata de problemas multifacetados que exigem o cumprimento simultâneo de várias condições. Todo CSP é composto por três elementos essenciais:
- Variáveis: Entidades que exigem atribuições de valores
- Domínios: Conjuntos de valores possíveis para cada variável
- Restrições: Regras que limitam as atribuições válidas de variáveis
O objetivo final do CSP envolve a identificação de atribuições de valores que satisfaçam todas as restrições impostas.
Considere os aplicativos de agendamento em que as variáveis representam tarefas, os domínios indicam os intervalos de tempo disponíveis e as restrições especificam as dependências das tarefas. Enquadrar esses cenários como CSPs permite a aplicação de algoritmos especializados para gerar programações compatíveis com as restrições.
Especificação de variáveis e domínios
As variáveis formam os elementos fundamentais em qualquer CSP, representando quantidades desconhecidas que exigem determinação. A notação convencional emprega rótulos em ordem alfabética (A, B, C etc.). Cada variável está associada a um domínio - o conjunto completo de valores permitidos que ela pode assumir. Os domínios podem conter valores numéricos, símbolos ou outros tipos de dados.
Por exemplo, um domínio numérico pode incluir {1, 2, 3, 4}, restringindo as variáveis a esses quatro valores inteiros.
Ao definir variáveis e domínios, certifique-se de que os domínios reflitam com precisão os intervalos de valores realistas das variáveis correspondentes. A definição precisa do domínio agiliza a solução de problemas ao restringir o espaço de busca de soluções. Nos cenários de gerenciamento da força de trabalho, as variáveis que representam a contagem de funcionários devem ter domínios inteiros não negativos. A especificação clara de variáveis e domínios estabelece a base para a formulação de restrições e a geração de soluções subsequentes.
Compreensão das restrições
As restrições estabelecem regras relacionais que regem as interações das variáveis, especificando combinações de valores permitidos. Essas restrições capturam os requisitos essenciais do problema e garantem a validade da solução. As restrições se manifestam de várias formas, incluindo expressões matemáticas, declarações lógicas ou representações simbólicas.
As variedades comuns de restrições incluem:
- Restrições de igualdade: Impõem valores idênticos entre variáveis (por exemplo, A = D)
- Restrições de desigualdade: Impõem valores diferentes entre as variáveis (por exemplo, A ≠ B)
- Restrições de intervalo: Limitam os valores das variáveis dentro dos limites especificados (por exemplo, C
Construção de gráficos de restrições
Construção de gráficos de restrições
Os gráficos de restrições fornecem representações visuais de CSP por meio de nós (variáveis) e bordas (restrições). A criação desses gráficos melhora a compreensão do problema e o desenvolvimento da estratégia de solução. Siga estas etapas de construção:
Criação de nós: Gere nós de gráficos para cada variável, rotulando-os adequadamente
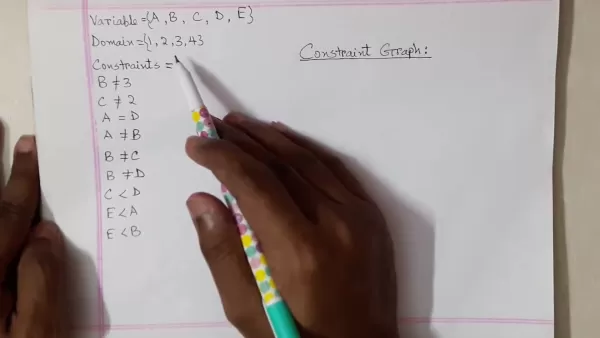
Implementação de bordas: Conecte os pares de variáveis restritas com bordas rotuladas indicando os tipos de restrição
Simplificação do gráfico: Otimizar o gráfico removendo bordas redundantes e consolidando nós equivalentes
Esse processo produz uma representação visual do problema adequada para a aplicação de vários algoritmos de solução baseados em gráficos.
Análise de gráficos de restrições
Os gráficos de restrições construídos permitem uma análise criteriosa do problema por meio de um exame estrutural. A análise do gráfico se concentra em:
- Componentes conectados: A identificação de subgrafos independentes permite a decomposição do problema
- Detecção de ciclos: O reconhecimento de dependências circulares destaca a complexidade do problema
- Avaliação do grau: Os nós com várias bordas representam variáveis críticas
O exame minucioso do gráfico revela insights valiosos sobre o problema, informando estratégias de solução eficazes por meio de inspeção visual e algoritmos especializados.
Guia de construção de gráficos de restrições
Etapa 1: Definição de variável e domínio
Comece identificando explicitamente todas as variáveis do problema e estabelecendo seus respectivos domínios. Por exemplo, cenários de coloração de mapas designariam regiões como variáveis e cores disponíveis como domínios. A especificação precisa do domínio, refletindo opções de valores realistas, simplifica o desenvolvimento subsequente de restrições.
Etapa 2: Formulação de restrições
Desenvolva restrições que regem as relações entre as variáveis por meio de expressões matemáticas ou lógicas não ambíguas. Considere vários tipos de restrições, incluindo igualdade, desigualdade e restrições de intervalo ao capturar os requisitos do problema.
Etapa 3: Renderização de gráficos
Traduza o CSP em formato visual construindo nós para variáveis e bordas para restrições. Empregue estilos de borda distintos para diferentes tipos de restrições para melhorar a legibilidade. Essa transformação de relações abstratas em visualização concreta facilita a análise do problema.
Etapa 4: otimização e análise de gráficos
Implemente técnicas de simplificação de gráficos para aumentar a clareza e, ao mesmo tempo, manter a integridade do problema. Aplique a análise teórica do gráfico para identificar oportunidades de solução de problemas por meio de componentes conectados, ciclos e nós críticos. Esse exame estruturado dá suporte à geração de soluções eficientes.
Considerações práticas
Seleção de software de CSP
As ferramentas de solução de CSP variam de ofertas de código aberto a ofertas comerciais com recursos variados. As opções de código aberto são adequadas para aplicações experimentais e de pequena escala, mas podem exigir conhecimento técnico especializado. As soluções comerciais oferecem funcionalidade robusta a preços correspondentes, com modelos de preços que incluem licenciamento baseado no usuário e assinaturas de nuvem.
Vantagens do Constraint Graph
Os benefícios incluem:
- Visualização aprimorada do problema
- Análise simplificada de relações
- Compatibilidade com algoritmos de gráficos
- Melhoria na comunicação da equipe
Limitações do Constraint Graph
Possíveis desvantagens:
- Tempo de construção para problemas grandes
- Requisitos de conhecimento em teoria dos grafos
- Desafios de representação de restrições complexas
- Desordem visual com interconexões densas
Aplicativos CSP
Implementações no mundo real
Os CSPs encontram aplicação em vários domínios:
- Agendamento: Otimização do sequenciamento de tarefas com restrições
- Alocação de recursos: Distribuição eficiente de ativos limitados
- Configuração: Projetar sistemas que atendam a requisitos específicos
- Planejamento: Desenvolvimento de sequências de ações para atingir objetivos
As implementações concretas incluem programação de linhas aéreas, gerenciamento de recursos hospitalares, planejamento de caminhos robóticos e configuração de sistemas de computador.
Perguntas frequentes
Quais são os benefícios dos gráficos de restrições?
Os gráficos de restrições oferecem várias vantagens, incluindo visualização intuitiva do problema, análise simplificada de relações e compatibilidade com algoritmos de gráficos estabelecidos. O formato visual aprimora a compreensão da estrutura do problema e facilita a identificação de abordagens de solução eficazes.
Como os domínios variáveis devem ser selecionados?
A seleção de domínios apropriados exige o equilíbrio entre abrangência e especificidade. Os domínios devem abranger todos os valores válidos possíveis sem incluir opções inválidas, considerando cuidadosamente a natureza da variável e as restrições do problema.
Quais técnicas resolvem CSPs de forma eficaz?
Os métodos eficazes de solução de CSPs incluem pesquisa de backtracking, propagação de restrições e heurística de ordenação de variáveis. A combinação dessas estratégias permite a exploração eficiente do espaço de solução e, ao mesmo tempo, garante a conformidade com as restrições.
A IA revoluciona a genômica: AlphaGenome revela os segredos ocultos do DNA
Embora o DNA humano contenha aproximadamente 3 bilhões de letras genéticas, os cientistas decodificaram apenas uma fração desse projeto biológico. A maior parte do nosso genoma - particularmente os 98
8BitDo revela o controlador Pro 3 com botões intercambiáveis e personalizáveis
A 8BitDo revela seu aguardado controle sem fio Pro 3, marcando a primeira grande atualização desde o modelo Pro 2 de 2021. Diferentemente dos recentes layouts no estilo Nintendo vistos no controle Ult
Revolucionando o acesso aos dados: Chat alimentado por IA para bancos de dados relacionais sem SQL
A tecnologia revolucionária de IA agora permite que qualquer pessoa interaja com bancos de dados relacionais usando linguagem cotidiana, sem necessidade de conhecimento especializado em SQL. Essa abor
