Master Constraint Graphs: Ein einfacher Problemlösungsleitfaden
Constraint-Graphen dienen als unschätzbare visuelle Hilfsmittel für die Lösung von Constraint-Satisfaction-Problemen (CSPs) in verschiedenen Disziplinen. Dieser praktische Leitfaden gliedert den Prozess der Konstruktion von Constraint-Graphen in klare, überschaubare Schritte, die sowohl für Neulinge als auch für erfahrene Experten geeignet sind. Wir untersuchen die Kernbausteine von CSPs - Variablen, Domänen und Einschränkungen - bevor wir ihre grafische Darstellung veranschaulichen. Die Entwicklung von Kenntnissen über Constraint-Graphen ermöglicht es Ihnen, komplizierte Probleme effizient zu lösen, indem Sie die Beziehungen zwischen Variablen und ihren potenziellen Werten abbilden.
Wichtige Punkte
Constraint-Diagramme bieten visuelle Klarheit bei der Lösung von Constraint-Problemen
Variablen enthalten Domänensätze, die mögliche Werte definieren, die sie annehmen können
Constraints legen Regeln für die Zuweisung von Variablenwerten fest
Die Knoten des Graphen entsprechen den Variablen, während die Kanten die Constraints darstellen.
Die Konstruktion von Constraint-Graphen verdeutlicht die Zusammenhänge zwischen den Variablen
Grundlagen von Constraint-Satisfaction-Problemen
Verständnis von Constraint-Satisfaction-Problemen
Bei Constraint Satisfaction Problems (CSPs) geht es darum, Wertzuweisungen für Variablen zu finden, die bestimmte Bedingungen erfüllen. Diese mathematischen Modelle kommen überall in der künstlichen Intelligenz, im Operations Research und in der Softwareentwicklung vor. Das Verständnis der CSP-Grundlagen erweist sich als wesentlich, wenn es um vielschichtige Probleme geht, die die gleichzeitige Erfüllung mehrerer Bedingungen erfordern. Jedes CSP besteht aus drei wesentlichen Elementen:
- Variablen: Entitäten, denen Werte zugewiesen werden müssen
- Domänen: Mögliche Wertemengen für jede Variable
- Constraints: Regeln zur Begrenzung gültiger Variablenzuweisungen
Das ultimative CSP-Ziel besteht in der Identifizierung von Wertzuweisungen, die alle auferlegten Beschränkungen erfüllen.

Man denke an Planungsanwendungen, bei denen Variablen Aufgaben darstellen, Domänen verfügbare Zeitfenster bezeichnen und Constraints Aufgabenabhängigkeiten spezifizieren. Die Darstellung solcher Szenarien als CSPs ermöglicht die Anwendung spezialisierter Algorithmen zur Generierung von Constraint-konformen Zeitplänen.
Spezifizierung von Variablen und Domänen
Variablen bilden die grundlegenden Elemente in jedem CSP und stellen unbekannte Größen dar, die bestimmt werden müssen. Die herkömmliche Notation verwendet alphabetische Bezeichnungen (A, B, C, usw.). Jede Variable ist mit einer Domäne verknüpft - der vollständigen Menge zulässiger Werte, die sie annehmen kann. Domänen können numerische Werte, Symbole oder andere Datentypen enthalten.

Eine numerische Domäne könnte beispielsweise {1, 2, 3, 4} enthalten und die Variablen auf diese vier ganzzahligen Werte beschränken.
Achten Sie bei der Definition von Variablen und Domänen darauf, dass die Domänen die realistischen Wertebereiche für die entsprechenden Variablen genau widerspiegeln. Eine genaue Definition der Domäne rationalisiert die Problemlösung, indem sie den Lösungssuchraum eingrenzt. In Szenarien zur Personalverwaltung sollten Variablen, die die Anzahl der Mitarbeiter darstellen, nicht-negative ganzzahlige Domänen besitzen. Eine klare Variablen- und Domänenspezifikation bildet die Grundlage für die anschließende Formulierung von Einschränkungen und die Generierung von Lösungen.
Verstehen von Constraints
Constraints legen relationale Regeln für die Interaktion von Variablen fest, indem sie zulässige Wertkombinationen spezifizieren. Diese Einschränkungen erfassen die wesentlichen Anforderungen des Problems und garantieren gleichzeitig die Gültigkeit der Lösung. Constraints manifestieren sich in verschiedenen Formen, einschließlich mathematischer Ausdrücke, logischer Aussagen oder symbolischer Darstellungen.

Gängige Constraint-Varianten sind:
- Gleichheitsbeschränkungen: Erzwingen identische Werte zwischen Variablen (z. B. A = D)
- Ungleichheitsbeschränkungen: Erzwingen unterschiedliche Werte zwischen den Variablen (z. B. A ≠ B)
- Bereichsbeschränkungen: Begrenzen die Variablenwerte innerhalb bestimmter Grenzen (z. B. C
Konstruktion von Constraint-Graphen
Aufbau von Constraint-Graphen
Constraint-Graphen bieten visuelle CSP-Darstellungen durch Knoten (Variablen) und Kanten (Constraints). Die Erstellung solcher Graphen verbessert das Problemverständnis und die Entwicklung von Lösungsstrategien. Befolgen Sie diese Konstruktionsschritte:
Knotenerstellung: Erzeugen Sie Graphknoten für jede Variable und beschriften Sie sie entsprechend
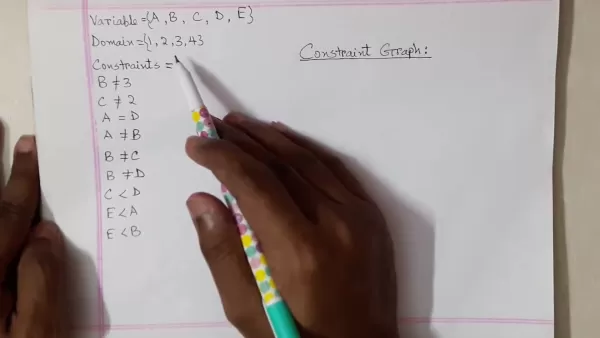
Implementierung von Kanten: Verbinden Sie gebundene Variablenpaare mit beschrifteten Kanten, die die Art der Beschränkung angeben.
Vereinfachung des Graphen: Optimieren des Graphen durch Entfernen überflüssiger Kanten und Zusammenfassen gleichwertiger Knoten
Dieser Prozess führt zu einer visuellen Problemdarstellung, die sich für die Anwendung verschiedener graphbasierter Lösungsalgorithmen eignet.
Analyse von Constraint-Graphen
Konstruierte Constraint-Graphen ermöglichen eine aufschlussreiche Problemanalyse durch strukturelle Untersuchung. Die Graphenanalyse konzentriert sich auf:
- Verbundene Komponenten: Die Identifizierung unabhängiger Teilgraphen ermöglicht die Dekomposition des Problems
- Erkennung von Kreisläufen: Das Erkennen von zirkulären Abhängigkeiten verdeutlicht die Komplexität des Problems
- Bewertung des Grades: Knoten mit zahlreichen Kanten stellen kritische Variablen dar
Eine gründliche Untersuchung des Graphen bringt wertvolle Erkenntnisse über das Problem zutage, die durch visuelle Inspektion und spezialisierte Algorithmen zu effektiven Lösungsstrategien führen.
Leitfaden für die Konstruktion von Constraint-Graphen
Schritt 1: Definition der Variablen und des Bereichs
Beginnen Sie damit, alle Problemvariablen explizit zu identifizieren und ihre jeweiligen Bereiche festzulegen. Bei Szenarien mit Kartenfärbung würden beispielsweise Regionen als Variablen und verfügbare Farben als Domänen bezeichnet werden. Eine präzise Domänenspezifikation, die realistische Wertoptionen widerspiegelt, vereinfacht die nachfolgende Entwicklung von Einschränkungen.

Schritt 2: Formulierung von Einschränkungen (Constraints)
Entwickeln Sie Constraints, die die Beziehungen zwischen den Variablen durch eindeutige mathematische oder logische Ausdrücke regeln. Berücksichtigen Sie verschiedene Constraint-Typen, einschließlich Gleichheits-, Ungleichheits- und Bereichs-Constraints, wenn Sie die Problemanforderungen erfassen.
Schritt 3: Graph-Rendering
Übersetzen Sie den CSP in eine visuelle Form, indem Sie Knoten für Variablen und Kanten für Constraints konstruieren. Um die Lesbarkeit zu verbessern, werden unterschiedliche Kantenstile für die verschiedenen Constraint-Typen verwendet. Diese Umwandlung von abstrakten Beziehungen in eine konkrete Visualisierung erleichtert die Problemanalyse.
Schritt 4: Optimierung und Analyse des Graphen
Implementieren Sie Techniken zur Vereinfachung des Graphen, um die Klarheit zu verbessern und gleichzeitig die Integrität des Problems zu erhalten. Wenden Sie eine graphentheoretische Analyse an, um Problemlösungsmöglichkeiten durch verbundene Komponenten, Zyklen und kritische Knoten zu identifizieren. Diese strukturierte Untersuchung unterstützt eine effiziente Lösungsgenerierung.
Praktische Überlegungen
Auswahl von CSP-Software
CSP-Lösungstools reichen von Open-Source- bis zu kommerziellen Angeboten mit unterschiedlichen Fähigkeiten. Open-Source-Optionen eignen sich für experimentelle und kleinere Anwendungen, erfordern aber möglicherweise technisches Fachwissen. Kommerzielle Lösungen bieten robuste Funktionalität zu entsprechenden Preisen, wobei die Preismodelle benutzerbasierte Lizenzen und Cloud-Abonnements umfassen.
Vorteile von Constraint Graph
Die Vorteile umfassen:
- Verbesserte Problemvisualisierung
- Vereinfachte Beziehungsanalyse
- Kompatibilität mit Graphenalgorithmen
- Verbesserte Teamkommunikation
Einschränkungen des Constraint-Graphen
Mögliche Nachteile:
- Konstruktionszeit für große Probleme
- Anforderungen an graphentheoretisches Fachwissen
- Komplexe Herausforderungen bei der Darstellung von Beschränkungen
- Visuelle Unübersichtlichkeit bei dichten Verflechtungen
CSP-Anwendungen
Real-World Implementierungen
CSPs finden in zahlreichen Bereichen Anwendung:
- Zeitplanung: Optimierung der Aufgabenreihenfolge unter Berücksichtigung von Beschränkungen
- Ressourcen-Zuweisung: Effiziente Verteilung von begrenzten Ressourcen
- Konfiguration: Entwerfen von Systemen, die bestimmte Anforderungen erfüllen
- Planung: Entwicklung von Handlungsabläufen zur Erreichung von Zielen
Zu den konkreten Anwendungen gehören die Planung von Fluglinien, die Verwaltung von Krankenhausressourcen, die Planung von Roboterbahnen und die Konfiguration von Computersystemen.
Häufig gestellte Fragen
Welche Vorteile bieten Constraint-Graphen?
Constraint-Graphen bieten mehrere Vorteile, darunter eine intuitive Problemvisualisierung, eine vereinfachte Beziehungsanalyse und die Kompatibilität mit etablierten Graphenalgorithmen. Das visuelle Format verbessert das Verständnis der Problemstruktur und erleichtert die Identifizierung effektiver Lösungsansätze.
Wie sollten variable Domänen ausgewählt werden?
Die Auswahl geeigneter Domänen erfordert ein Gleichgewicht zwischen Vollständigkeit und Spezifität. Die Domänen sollten alle möglichen gültigen Werte umfassen, ohne ungültige Optionen einzuschließen, wobei die Art der Variablen und die Problemeinschränkungen sorgfältig zu berücksichtigen sind.
Welche Techniken lösen CSPs effektiv?
Zu den wirksamen CSP-Lösungsmethoden gehören Backtracking-Suche, Constraint-Propagation und Heuristiken zur Variablenanordnung. Die Kombination dieser Strategien ermöglicht eine effiziente Erkundung des Lösungsraums und gewährleistet gleichzeitig die Einhaltung von Nebenbedingungen.
Verwandter Artikel
 AI revolutioniert die Genomik: AlphaGenome entschlüsselt die verborgenen Geheimnisse der DNA
Obwohl die menschliche DNA etwa 3 Milliarden genetische Buchstaben enthält, haben Wissenschaftler nur einen Bruchteil dieses biologischen Bauplans entschlüsselt. Der Großteil unseres Genoms - insbeson
AI revolutioniert die Genomik: AlphaGenome entschlüsselt die verborgenen Geheimnisse der DNA
Obwohl die menschliche DNA etwa 3 Milliarden genetische Buchstaben enthält, haben Wissenschaftler nur einen Bruchteil dieses biologischen Bauplans entschlüsselt. Der Großteil unseres Genoms - insbeson
 8BitDo stellt den Pro 3 Controller mit anpassbaren, austauschbaren Knöpfen vor
8BitDo stellt den mit Spannung erwarteten kabellosen Pro 3-Controller vor, der die erste größere Aktualisierung seit dem Pro 2-Modell von 2021 darstellt. Der Pro 3 weicht vom Nintendo-Layout des Ultim
8BitDo stellt den Pro 3 Controller mit anpassbaren, austauschbaren Knöpfen vor
8BitDo stellt den mit Spannung erwarteten kabellosen Pro 3-Controller vor, der die erste größere Aktualisierung seit dem Pro 2-Modell von 2021 darstellt. Der Pro 3 weicht vom Nintendo-Layout des Ultim
 Datenzugriff revolutionieren: KI-gestützter Chat für relationale Datenbanken ohne SQL
Dank revolutionärer KI-Technologie kann nun jeder mit relationalen Datenbanken interagieren, indem er die Alltagssprache verwendet - ohne spezielle SQL-Kenntnisse. Dieser innovative Ansatz verwandelt
Kommentare (0)
0/200
Datenzugriff revolutionieren: KI-gestützter Chat für relationale Datenbanken ohne SQL
Dank revolutionärer KI-Technologie kann nun jeder mit relationalen Datenbanken interagieren, indem er die Alltagssprache verwendet - ohne spezielle SQL-Kenntnisse. Dieser innovative Ansatz verwandelt
Kommentare (0)
0/200
Constraint-Graphen dienen als unschätzbare visuelle Hilfsmittel für die Lösung von Constraint-Satisfaction-Problemen (CSPs) in verschiedenen Disziplinen. Dieser praktische Leitfaden gliedert den Prozess der Konstruktion von Constraint-Graphen in klare, überschaubare Schritte, die sowohl für Neulinge als auch für erfahrene Experten geeignet sind. Wir untersuchen die Kernbausteine von CSPs - Variablen, Domänen und Einschränkungen - bevor wir ihre grafische Darstellung veranschaulichen. Die Entwicklung von Kenntnissen über Constraint-Graphen ermöglicht es Ihnen, komplizierte Probleme effizient zu lösen, indem Sie die Beziehungen zwischen Variablen und ihren potenziellen Werten abbilden.
Wichtige Punkte
Constraint-Diagramme bieten visuelle Klarheit bei der Lösung von Constraint-Problemen
Variablen enthalten Domänensätze, die mögliche Werte definieren, die sie annehmen können
Constraints legen Regeln für die Zuweisung von Variablenwerten fest
Die Knoten des Graphen entsprechen den Variablen, während die Kanten die Constraints darstellen.
Die Konstruktion von Constraint-Graphen verdeutlicht die Zusammenhänge zwischen den Variablen
Grundlagen von Constraint-Satisfaction-Problemen
Verständnis von Constraint-Satisfaction-Problemen
Bei Constraint Satisfaction Problems (CSPs) geht es darum, Wertzuweisungen für Variablen zu finden, die bestimmte Bedingungen erfüllen. Diese mathematischen Modelle kommen überall in der künstlichen Intelligenz, im Operations Research und in der Softwareentwicklung vor. Das Verständnis der CSP-Grundlagen erweist sich als wesentlich, wenn es um vielschichtige Probleme geht, die die gleichzeitige Erfüllung mehrerer Bedingungen erfordern. Jedes CSP besteht aus drei wesentlichen Elementen:
- Variablen: Entitäten, denen Werte zugewiesen werden müssen
- Domänen: Mögliche Wertemengen für jede Variable
- Constraints: Regeln zur Begrenzung gültiger Variablenzuweisungen
Das ultimative CSP-Ziel besteht in der Identifizierung von Wertzuweisungen, die alle auferlegten Beschränkungen erfüllen.

Man denke an Planungsanwendungen, bei denen Variablen Aufgaben darstellen, Domänen verfügbare Zeitfenster bezeichnen und Constraints Aufgabenabhängigkeiten spezifizieren. Die Darstellung solcher Szenarien als CSPs ermöglicht die Anwendung spezialisierter Algorithmen zur Generierung von Constraint-konformen Zeitplänen.
Spezifizierung von Variablen und Domänen
Variablen bilden die grundlegenden Elemente in jedem CSP und stellen unbekannte Größen dar, die bestimmt werden müssen. Die herkömmliche Notation verwendet alphabetische Bezeichnungen (A, B, C, usw.). Jede Variable ist mit einer Domäne verknüpft - der vollständigen Menge zulässiger Werte, die sie annehmen kann. Domänen können numerische Werte, Symbole oder andere Datentypen enthalten.

Eine numerische Domäne könnte beispielsweise {1, 2, 3, 4} enthalten und die Variablen auf diese vier ganzzahligen Werte beschränken.
Achten Sie bei der Definition von Variablen und Domänen darauf, dass die Domänen die realistischen Wertebereiche für die entsprechenden Variablen genau widerspiegeln. Eine genaue Definition der Domäne rationalisiert die Problemlösung, indem sie den Lösungssuchraum eingrenzt. In Szenarien zur Personalverwaltung sollten Variablen, die die Anzahl der Mitarbeiter darstellen, nicht-negative ganzzahlige Domänen besitzen. Eine klare Variablen- und Domänenspezifikation bildet die Grundlage für die anschließende Formulierung von Einschränkungen und die Generierung von Lösungen.
Verstehen von Constraints
Constraints legen relationale Regeln für die Interaktion von Variablen fest, indem sie zulässige Wertkombinationen spezifizieren. Diese Einschränkungen erfassen die wesentlichen Anforderungen des Problems und garantieren gleichzeitig die Gültigkeit der Lösung. Constraints manifestieren sich in verschiedenen Formen, einschließlich mathematischer Ausdrücke, logischer Aussagen oder symbolischer Darstellungen.

Gängige Constraint-Varianten sind:
- Gleichheitsbeschränkungen: Erzwingen identische Werte zwischen Variablen (z. B. A = D)
- Ungleichheitsbeschränkungen: Erzwingen unterschiedliche Werte zwischen den Variablen (z. B. A ≠ B)
- Bereichsbeschränkungen: Begrenzen die Variablenwerte innerhalb bestimmter Grenzen (z. B. C
Konstruktion von Constraint-Graphen
Aufbau von Constraint-Graphen
Constraint-Graphen bieten visuelle CSP-Darstellungen durch Knoten (Variablen) und Kanten (Constraints). Die Erstellung solcher Graphen verbessert das Problemverständnis und die Entwicklung von Lösungsstrategien. Befolgen Sie diese Konstruktionsschritte:
Knotenerstellung: Erzeugen Sie Graphknoten für jede Variable und beschriften Sie sie entsprechend
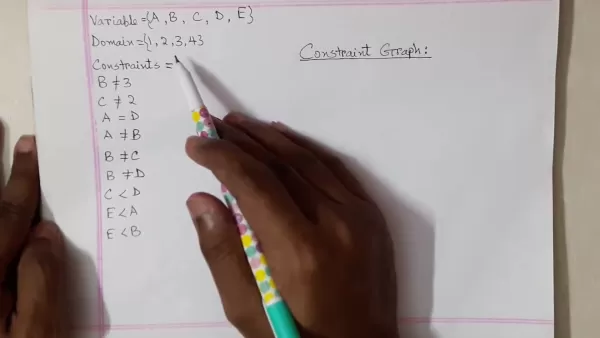
Implementierung von Kanten: Verbinden Sie gebundene Variablenpaare mit beschrifteten Kanten, die die Art der Beschränkung angeben.
Vereinfachung des Graphen: Optimieren des Graphen durch Entfernen überflüssiger Kanten und Zusammenfassen gleichwertiger Knoten
Dieser Prozess führt zu einer visuellen Problemdarstellung, die sich für die Anwendung verschiedener graphbasierter Lösungsalgorithmen eignet.
Analyse von Constraint-Graphen
Konstruierte Constraint-Graphen ermöglichen eine aufschlussreiche Problemanalyse durch strukturelle Untersuchung. Die Graphenanalyse konzentriert sich auf:
- Verbundene Komponenten: Die Identifizierung unabhängiger Teilgraphen ermöglicht die Dekomposition des Problems
- Erkennung von Kreisläufen: Das Erkennen von zirkulären Abhängigkeiten verdeutlicht die Komplexität des Problems
- Bewertung des Grades: Knoten mit zahlreichen Kanten stellen kritische Variablen dar
Eine gründliche Untersuchung des Graphen bringt wertvolle Erkenntnisse über das Problem zutage, die durch visuelle Inspektion und spezialisierte Algorithmen zu effektiven Lösungsstrategien führen.
Leitfaden für die Konstruktion von Constraint-Graphen
Schritt 1: Definition der Variablen und des Bereichs
Beginnen Sie damit, alle Problemvariablen explizit zu identifizieren und ihre jeweiligen Bereiche festzulegen. Bei Szenarien mit Kartenfärbung würden beispielsweise Regionen als Variablen und verfügbare Farben als Domänen bezeichnet werden. Eine präzise Domänenspezifikation, die realistische Wertoptionen widerspiegelt, vereinfacht die nachfolgende Entwicklung von Einschränkungen.

Schritt 2: Formulierung von Einschränkungen (Constraints)
Entwickeln Sie Constraints, die die Beziehungen zwischen den Variablen durch eindeutige mathematische oder logische Ausdrücke regeln. Berücksichtigen Sie verschiedene Constraint-Typen, einschließlich Gleichheits-, Ungleichheits- und Bereichs-Constraints, wenn Sie die Problemanforderungen erfassen.
Schritt 3: Graph-Rendering
Übersetzen Sie den CSP in eine visuelle Form, indem Sie Knoten für Variablen und Kanten für Constraints konstruieren. Um die Lesbarkeit zu verbessern, werden unterschiedliche Kantenstile für die verschiedenen Constraint-Typen verwendet. Diese Umwandlung von abstrakten Beziehungen in eine konkrete Visualisierung erleichtert die Problemanalyse.
Schritt 4: Optimierung und Analyse des Graphen
Implementieren Sie Techniken zur Vereinfachung des Graphen, um die Klarheit zu verbessern und gleichzeitig die Integrität des Problems zu erhalten. Wenden Sie eine graphentheoretische Analyse an, um Problemlösungsmöglichkeiten durch verbundene Komponenten, Zyklen und kritische Knoten zu identifizieren. Diese strukturierte Untersuchung unterstützt eine effiziente Lösungsgenerierung.
Praktische Überlegungen
Auswahl von CSP-Software
CSP-Lösungstools reichen von Open-Source- bis zu kommerziellen Angeboten mit unterschiedlichen Fähigkeiten. Open-Source-Optionen eignen sich für experimentelle und kleinere Anwendungen, erfordern aber möglicherweise technisches Fachwissen. Kommerzielle Lösungen bieten robuste Funktionalität zu entsprechenden Preisen, wobei die Preismodelle benutzerbasierte Lizenzen und Cloud-Abonnements umfassen.
Vorteile von Constraint Graph
Die Vorteile umfassen:
- Verbesserte Problemvisualisierung
- Vereinfachte Beziehungsanalyse
- Kompatibilität mit Graphenalgorithmen
- Verbesserte Teamkommunikation
Einschränkungen des Constraint-Graphen
Mögliche Nachteile:
- Konstruktionszeit für große Probleme
- Anforderungen an graphentheoretisches Fachwissen
- Komplexe Herausforderungen bei der Darstellung von Beschränkungen
- Visuelle Unübersichtlichkeit bei dichten Verflechtungen
CSP-Anwendungen
Real-World Implementierungen
CSPs finden in zahlreichen Bereichen Anwendung:
- Zeitplanung: Optimierung der Aufgabenreihenfolge unter Berücksichtigung von Beschränkungen
- Ressourcen-Zuweisung: Effiziente Verteilung von begrenzten Ressourcen
- Konfiguration: Entwerfen von Systemen, die bestimmte Anforderungen erfüllen
- Planung: Entwicklung von Handlungsabläufen zur Erreichung von Zielen
Zu den konkreten Anwendungen gehören die Planung von Fluglinien, die Verwaltung von Krankenhausressourcen, die Planung von Roboterbahnen und die Konfiguration von Computersystemen.
Häufig gestellte Fragen
Welche Vorteile bieten Constraint-Graphen?
Constraint-Graphen bieten mehrere Vorteile, darunter eine intuitive Problemvisualisierung, eine vereinfachte Beziehungsanalyse und die Kompatibilität mit etablierten Graphenalgorithmen. Das visuelle Format verbessert das Verständnis der Problemstruktur und erleichtert die Identifizierung effektiver Lösungsansätze.
Wie sollten variable Domänen ausgewählt werden?
Die Auswahl geeigneter Domänen erfordert ein Gleichgewicht zwischen Vollständigkeit und Spezifität. Die Domänen sollten alle möglichen gültigen Werte umfassen, ohne ungültige Optionen einzuschließen, wobei die Art der Variablen und die Problemeinschränkungen sorgfältig zu berücksichtigen sind.
Welche Techniken lösen CSPs effektiv?
Zu den wirksamen CSP-Lösungsmethoden gehören Backtracking-Suche, Constraint-Propagation und Heuristiken zur Variablenanordnung. Die Kombination dieser Strategien ermöglicht eine effiziente Erkundung des Lösungsraums und gewährleistet gleichzeitig die Einhaltung von Nebenbedingungen.
 8BitDo stellt den Pro 3 Controller mit anpassbaren, austauschbaren Knöpfen vor
8BitDo stellt den mit Spannung erwarteten kabellosen Pro 3-Controller vor, der die erste größere Aktualisierung seit dem Pro 2-Modell von 2021 darstellt. Der Pro 3 weicht vom Nintendo-Layout des Ultim
8BitDo stellt den Pro 3 Controller mit anpassbaren, austauschbaren Knöpfen vor
8BitDo stellt den mit Spannung erwarteten kabellosen Pro 3-Controller vor, der die erste größere Aktualisierung seit dem Pro 2-Modell von 2021 darstellt. Der Pro 3 weicht vom Nintendo-Layout des Ultim
 Datenzugriff revolutionieren: KI-gestützter Chat für relationale Datenbanken ohne SQL
Dank revolutionärer KI-Technologie kann nun jeder mit relationalen Datenbanken interagieren, indem er die Alltagssprache verwendet - ohne spezielle SQL-Kenntnisse. Dieser innovative Ansatz verwandelt
Datenzugriff revolutionieren: KI-gestützter Chat für relationale Datenbanken ohne SQL
Dank revolutionärer KI-Technologie kann nun jeder mit relationalen Datenbanken interagieren, indem er die Alltagssprache verwendet - ohne spezielle SQL-Kenntnisse. Dieser innovative Ansatz verwandelt